Progress Towards A Fully Functional Outer Sumcheck
This document loosely tracks progress on the streaming implementation of the spartan sumcheck. This pull request tracks our latest changes.
There should be no difference in performance between the linear
sum-check implementation and the streaming implementation if the
streaming schedule is LinearOnlySchedule defined here
Currently we are about 2.5x slower.
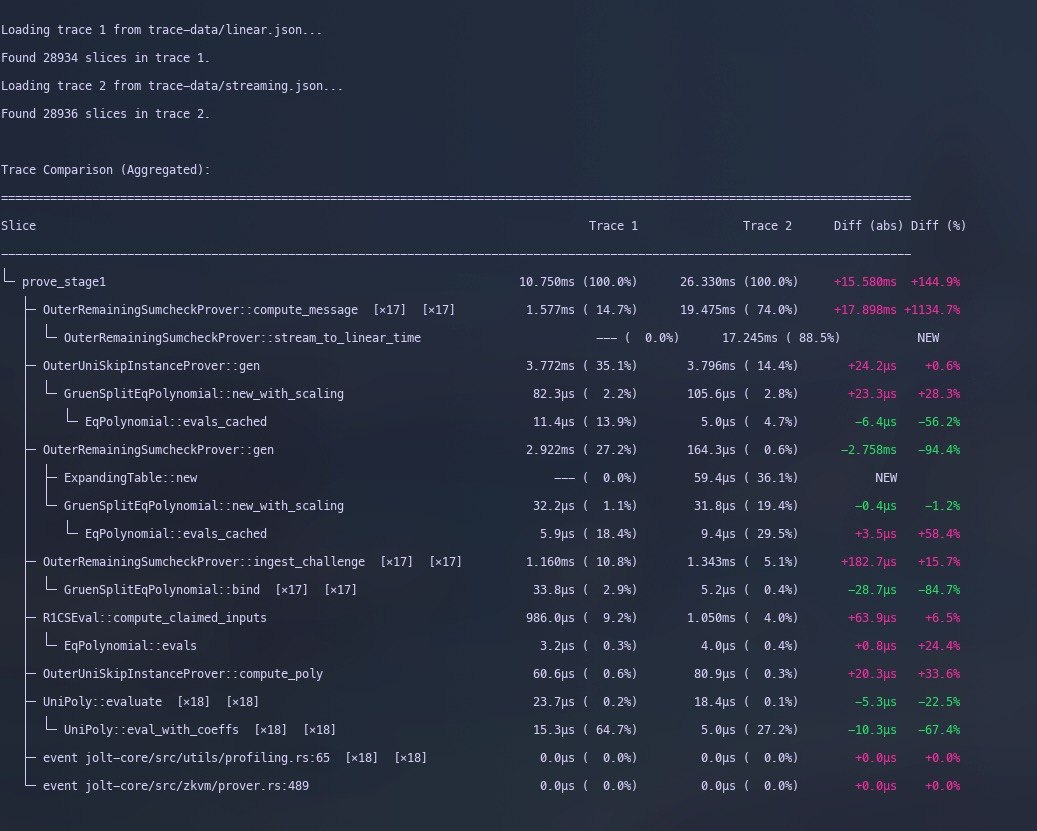
A closer inspection shows us that the entire slowdown is coming from
the stream_to_linear_time function.
Another notable difference is that in the Linear Sumcheck
OuterRemaingSumcheckProver::gen is considerably slower.
This is not an optimisation, but an artefact of moving code around. We
were initially manifesting Az and Bz, and
computing the first message inside of gen. Now we do this
in the compute_message function of the first round that is
in the linear phase of the sum-check schedule.
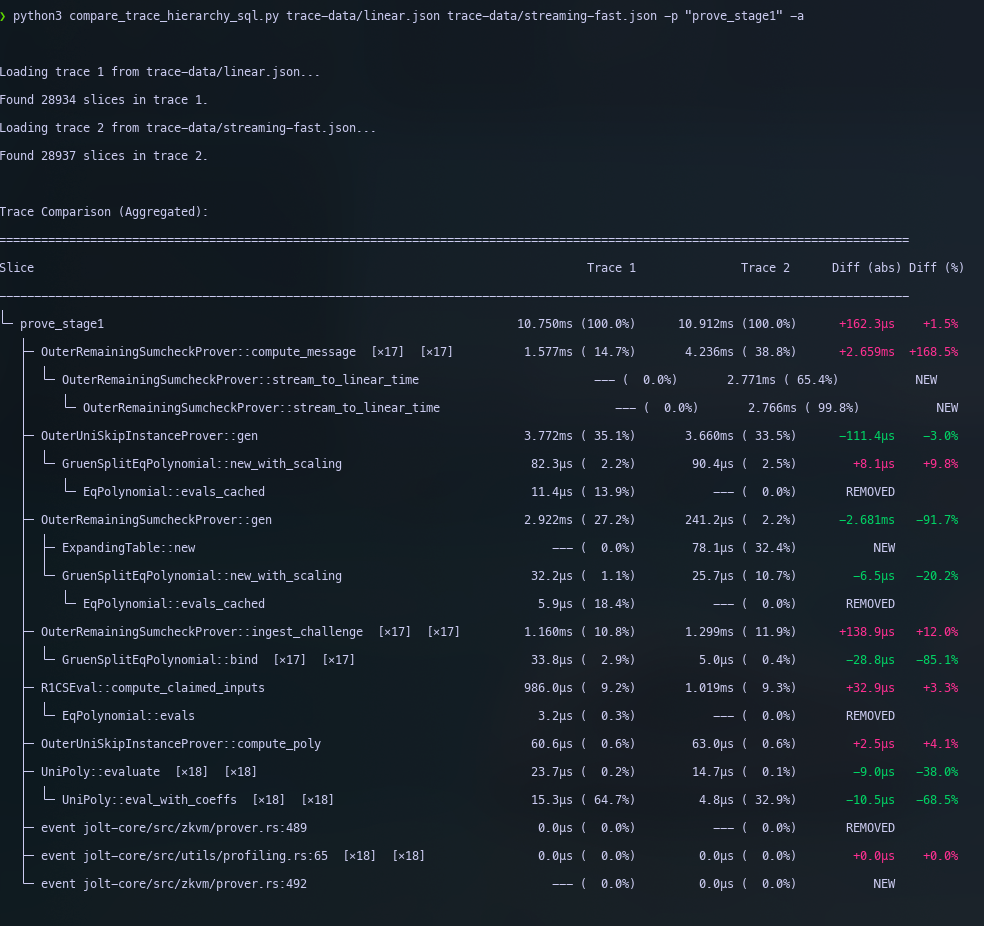
Fixing stream_to_linear() for round 0
If we are guaranteed that the first linear phase in the schedule is
round zero, then the optimisation is relatively easy. We just need to
adapt the compute_first_quadratic_evals_and_bound_polys
function. This immediately matches us with the linear sum-check (as was
the only thing that we needed to improve.) NOTE: We
also use the existing optimisations for small values. The code can be
found here
Each unit of work is described by the processing of an array of size \(2\sqrt{T}\) and there are \(\sqrt{T}\) such units being shared/stolen from inside the thread pool.
These evaluations were run while verifying the sha3
program which has \(\log_2 T = 16\).
When \(T\) is much larger, we need to
verify if this is still the right strategy or we need to chunk slightly
differently. Either ways, \(\log_2 T\)
can be at most \(30\), and we have seen
that processing an array of size \(2^{16}\) serially is not that much slower.
So this is something we should micro-optimise only if we have nothing
better to do.
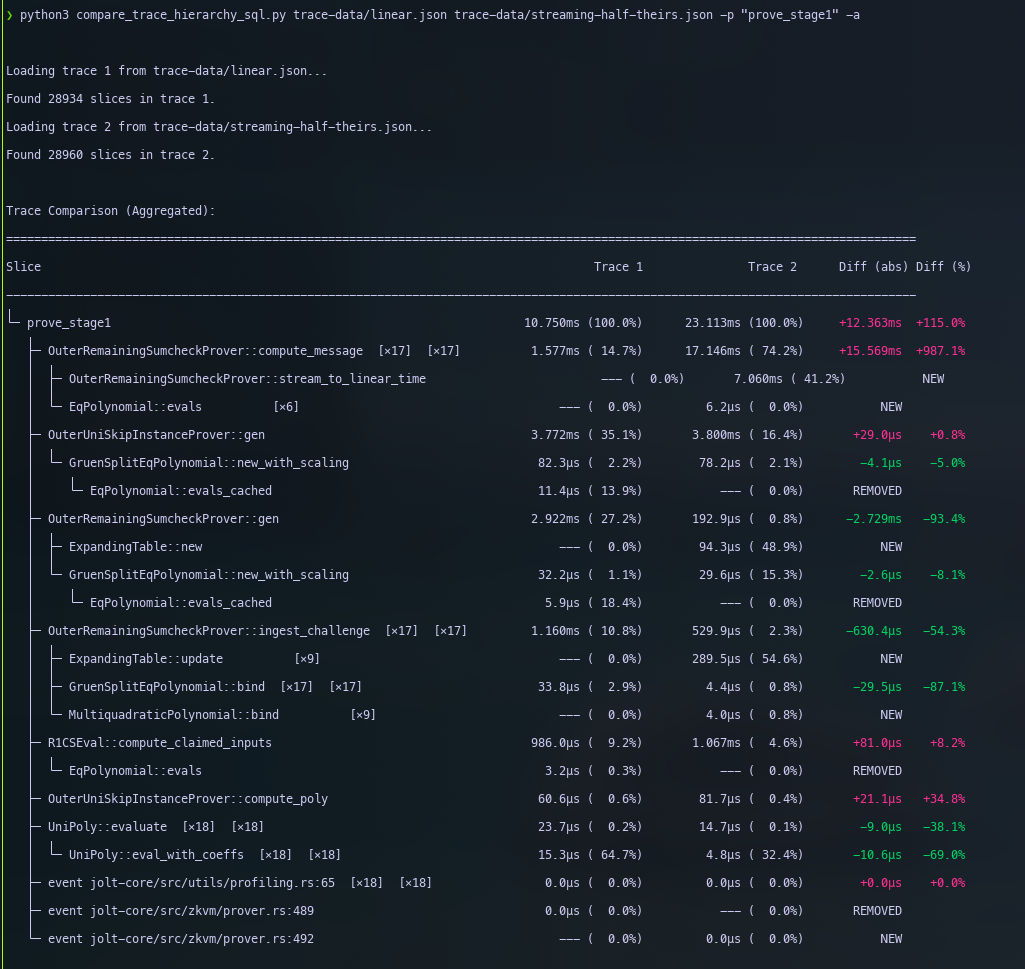
Fixing stream_to_linear() for any round
We’ve fixed the issue when the first linear round is the first round
of sum-check, but we have not yet optimised the code path for any other
streaming schedule. That is where the sum-check actually has a streaming
phase, and recomputing Az and Bz involves
accounting for a prefix of bound variables.
The only code path we have optimised so far is the
stream_to_linear() binding operation. In any streaming
schedule the compute_prover message includes special rounds
where we need to optimise the re-computation of the windows. Currently,
we have not yet verified that these are optimal. The numbers below just
describe our improvements to the stream_to_linear() phase
of the algorithm
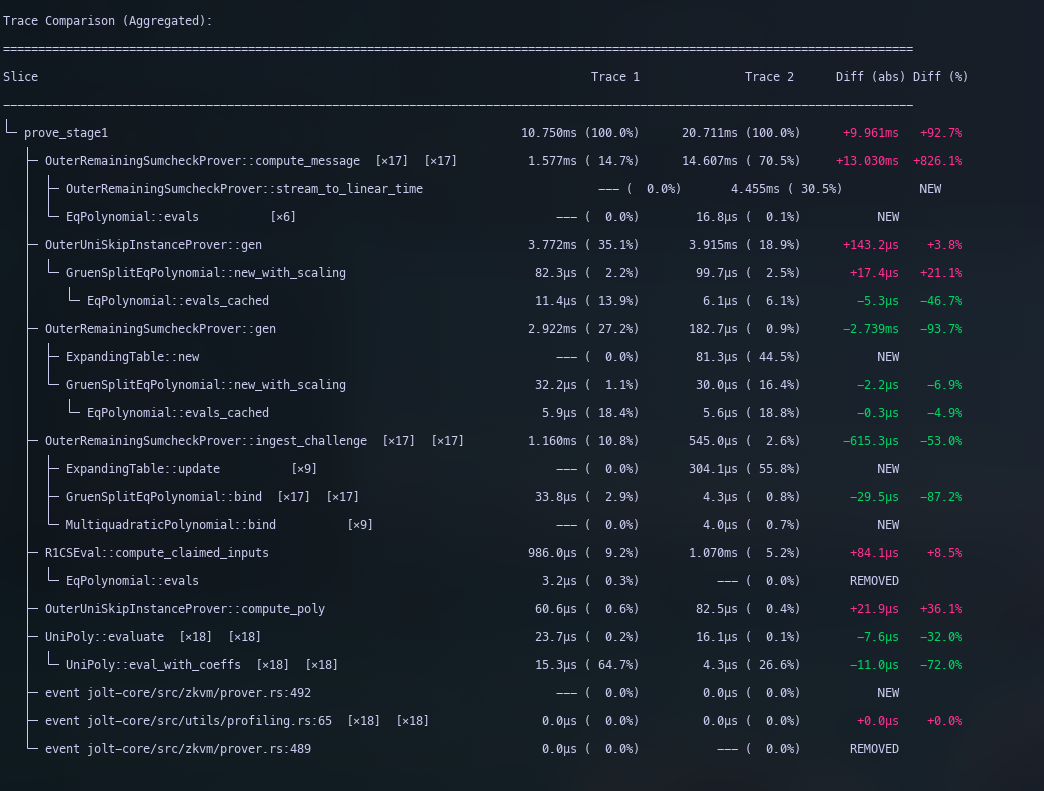
Towards this we investigate two solutions:
- Optimising the existing implementation which has a rather
complicated structure but includes small value optimisations. Observe
that the current
stream_to_linear_time()code only takes7msas opposed to the17mswe started with. Code
This is owing to us changing
// Final reductions once per j.
for j in 0..jlen {
let az_j = acc_az[j].barrett_reduce();
let bz_first_j = acc_bz_first[j].barrett_reduce();
let bz_second_j = acc_bz_second[j].barrett_reduce();
grid_az[j] = az_j;
grid_bz[j] = bz_first_j + bz_second_j;
}
to the following code. The unsafe block is because the
compiler does not realise we actually write to different parts of the
array.
let grid_az_ptr = grid_az.as_mut_ptr() as usize;
let grid_bz_ptr = grid_bz.as_mut_ptr() as usize;
let chunk_size = 4096;
let num_chunks = (jlen + chunk_size - 1) / chunk_size;
(0..num_chunks).into_par_iter().for_each(move |chunk_idx| {
let start = chunk_idx * chunk_size;
let end = (start + chunk_size).min(jlen);
let az_ptr = grid_az_ptr as *mut F;
let bz_ptr = grid_bz_ptr as *mut F;
for j in start..end {
let az_j = acc_az[j].barrett_reduce();
let bz_first_j = acc_bz_first[j].barrett_reduce();
let bz_second_j = acc_bz_second[j].barrett_reduce();
unsafe {
*az_ptr.add(j) = az_j;
*bz_ptr.add(j) = bz_first_j + bz_second_j;
}
}
});
- We write a simple parallel version without small value optimisation,
but one where we know the cache lines are well aligned. Notice that
stream_to_linear_timeis not as fast as ourlinear_scheduleversion, but it is still nearly twice as fast as the existing parallelised version. The reason it’s likely much faster is due to simplicity – we iterate over arrays just once. The reason it’s slower than the original version, is because in this version we need to multiply all the \(\text{eq}(r,x_r)\) polynomials, and additionally the window size is 3. So the chunking is not as nice and uniform. Still we loose about2ms, which in the grand scheme of things is negligible. Code
Next Steps
Unifying the API
This is what we the prover_message to look like, currently we have a much more verbose version.
fn compute_message(&mut self, round: usize, previous_claim: F) -> UniPoly<F> {
// If this is a window start, materialize the window grid
if self.schedule.is_window_start(round) {
self.compute_window_evals_for_new_window(round);
}
// Use the window grid to compute this round's prover message
self.get_prover_message_from_window_evals(previous_claim)
}