Phase King Through The Lens Of Gradecast
The write up is based on the blog post by Andrew Lewis-Pye and Ittai Abraham
The goal of this post is show that if f < n/3 then we can come up with a protocol \Pi (which is known as Phase King) that can solve byzantine agreement and therefore byzantine broadcast as well.
Gradecast Algorithm
First we describe the Gradecast algorithm.It’s a two stage algorithm where:
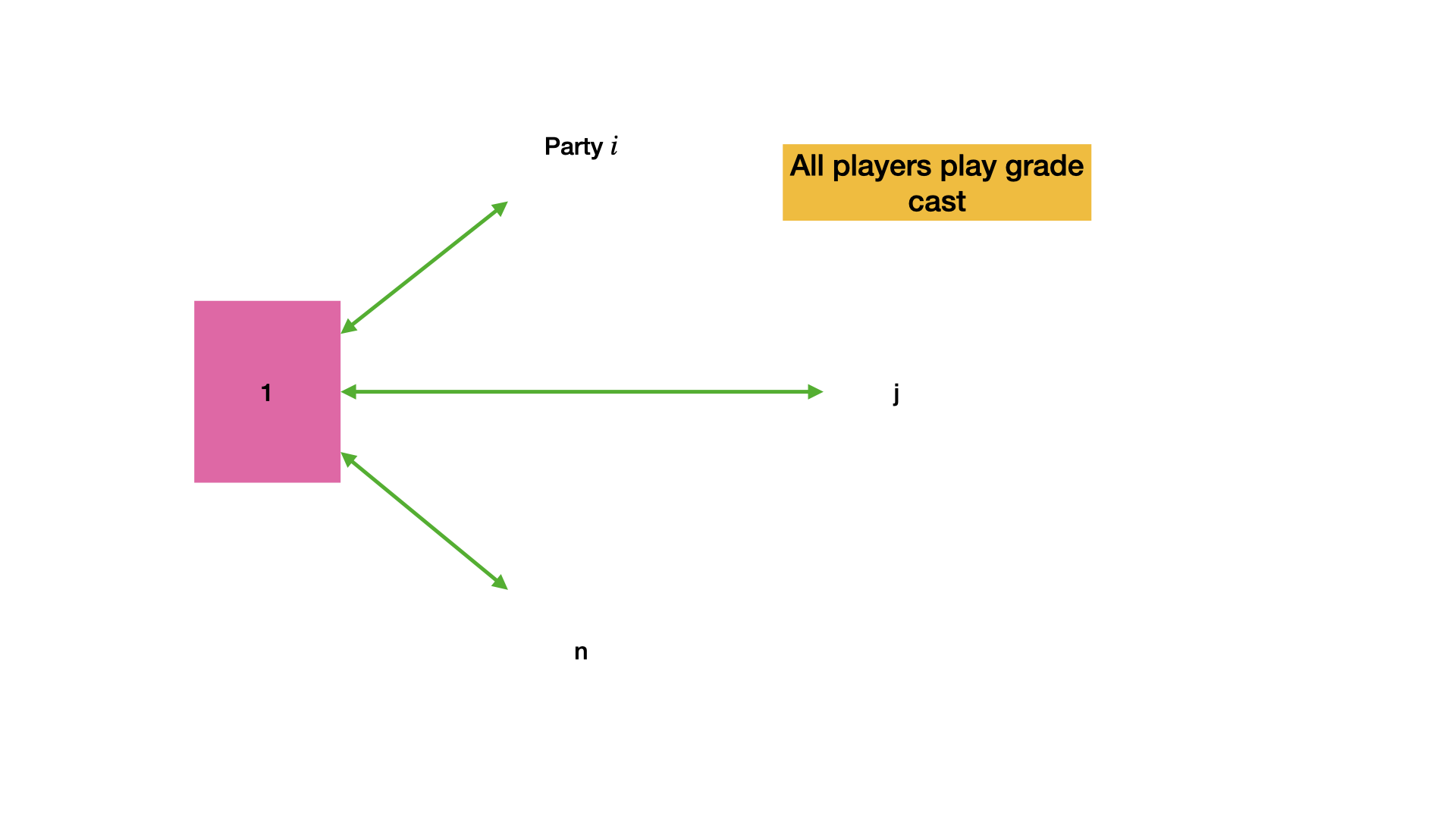
- First Stage: Each party i \in [n] is asked to broadcast its inputs v_i.
- Second Stage: If party i receives at least n-f messages that support b it broadcasts b to all other parties.
Output: At the end of this stage 2 if party i hears at least n-f messages in support of b it outputs \hat{v}_i = b with grade 2. Instead if it sees at least f+1 votes for message b it outputs \hat{v}_i = b with grade 1. If neither happens, it outputs \hat{v}_i = v_i with grade 0.
Below is an animation that visualises the above protocol. Click on arrows to see how protocol proceeds

Gradecast satisfies the following properties
If all honest parties have the same input value, then all of them output this value with grade 2.
If all the honest nodes have the same input v, then they all send v in round 1. Thus in step 2, each honest party will see at least n-f messages supporting v, and therefore themselves broadcast v. As every honest party broadcasts v in the second round and we are in the synchronous model, every honest party will see at least n-f messages supporting v after round 2. Therefore they all output v with grade 2.
No two honest parties send conflicting round 2 messages
Say honest player i receives n-f votes at the end of round 1 for value b from players A \subseteq [n], and honest player j receives n-f votes for b' from players B \subseteq [n]. As f < n/3, we must have at least one honest player in the intersection of A \cap B. Thus, this honest party votes twice in the first step, which it will not do (Contradiction!)
If an honest party outputs a value with grade 2, then all honest parties output this value.
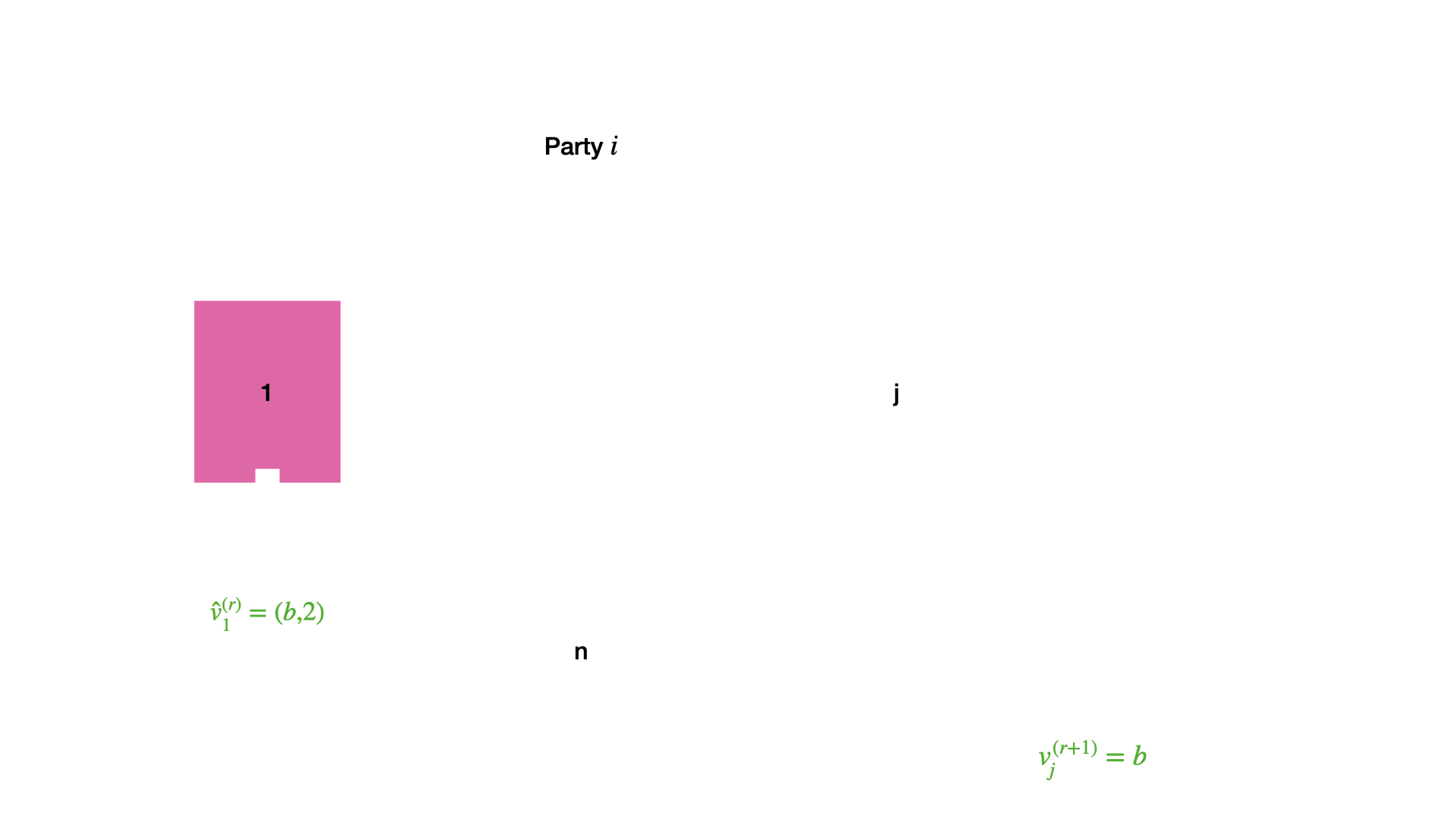
Let’s say an honest party i outputs (b,2). This implies that at the end of round 2, it receives at least n-f votes1 for the value b. Now consider any other honest party j \neq i. j must receive at least n-2f \geq f+1 votes2 for b at the end of the second round (See picture below).
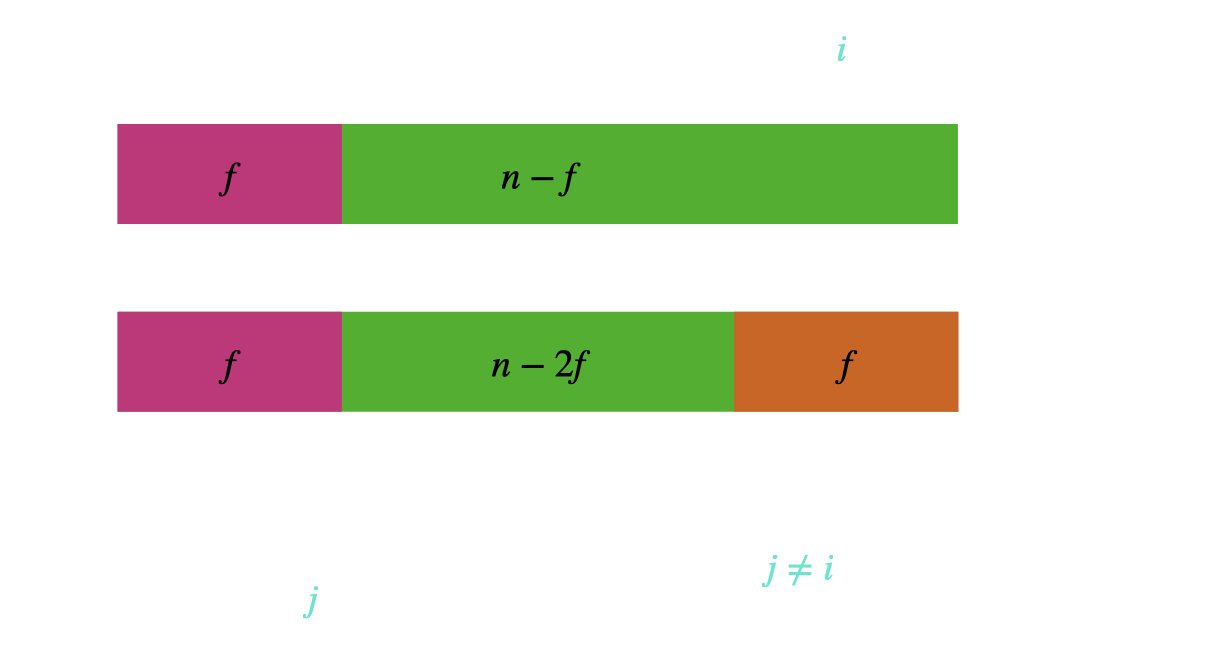
Ok, just because every honest party j \neq i receives at least n-2f \geq f+1 votes for b, we have not shown that it could not have received say at least f+1 votes for another value b' \neq b.
This is where weak agreement kicks in. For another honest party j \neq i to receive at least f+1 votes for b' \neq b, it would need at least 1 honest party to send b' which is not possible, as weak agreement says no two honest nodes send conflicting messages at the end of round 2.
What gradecast gives us is that if all honest parties have the same input, they all know of this fact by just looking at their output (if I see an output of with grade 2, then I know everything is good!). What happens when all honest players do not start with the same input? We show that if we run gradecast enough number of times we get everything we want.
Phase King (Click on arrows to see next steps)
Click on arrows to see how protocol proceeds
If all honest nodes start with input v, then by validity of gradecast all honest nodes will output v with grade 2. This means that the honest nodes ignore the king in each phase, and finally all output v as their output.
Note that as we have f+1 phases – at some point we will have an honest king. Unless the output of gradecast has grade 2, all honest nodes will pick the leaders output as their input their input for the next round. As the leader is honest we have that all of these nodes will have the same output.
For the honest node that does not copy the leader, it does not copy because, it has grade 2, but then by knowledge agreement of gradecast, all honest nodes have the same output as the honest node with grade 2. The leader is honest, so the leader and this node have the same value anyway.
Either this is the last phase, then we get agreement, or in the next phases – regardless of who is the leader, as all honest nodes have the same input – validity of gradecast kicks in – and eventually we will have agreement.